АННОТАЦИЯ
В статье анализируется проблема появления знаменитой пропорции « золотое отношение». Что может быть основанием этого явления — работа сознания, абстрактное мышление или законы Природы? Известно множество геометрических построений где отношение величин элементов геометрической фигуры дает знаменитую пропорцию. Но все эти построения не давали ответ на главный вопрос: о наличии функциональной зависимости аргумента и функции. Что является аргументом и что является функцией. В чем проявляется единство частей пространства при наличии такой пропорции. Большое множество фактов появления этой пропорции в отношении частей объектов свидетельствует о функциональных свойствах этого явления. Это явление может быть случайным в числовом множестве и может носить закономерный характер. Как известно из математики, случайные величины имеют различные значения в ограниченной области.
Это вынуждает оценивать числовую величину с определенным приближением. Такого рода процессы характерны для непредсказуемых событий. Но Природа целостна и устойчива по своему построению и имеет элементы красоты. Для сочетания множества элементов в пространстве требуется функциональная зависимость, результат которой является закономерным. Особенно необходима закономерность сочетания частей и целого в архитектуре. Пространственная среда в архитектуре требует технического решения, функционального решения организации и эстетического. В этом случае пропорция «золотое отношение» позволяет решать многообразие разноплановых задач. Древние геометры говорили: СМОТРИ. И это является основным направлением изложения материала.
ABSTRACT
In article the problem of emergence of the well-known proportion "extreme and mean ratio" is analyzed. What can be the basis of this phenomenon — work of consciousness, abstrakt thinking or laws of the Nature? The set of geometrical constructions is known where the relation of sizes of elements of geometrical figure gives the well-known proportion. But all these constructions did not give the answer to the main issue: about existence of the functional dependence of argument and function. What is argument and that is function. In what the unity of parts of space in the presence of such proportion is shown. The big set of the facts of emergence of this proportion concerning parts of objects testifies to the functional properties of this phenomenon. This phenomenon can be casual in a numerical set and can have natural character. As it is known from mathematics, random values have various values in restricted area. It forces to estimate a numerical value with a particular approximation.
Such processes are characteristic of unpredictable events. But the Nature is complete and steady on the construction and has beauty elements. The combination of a set of elements in space requires the functional dependence which result is natural. Regularity of a combination of parts and whole in architecture is especially necessary. The space environment in architecture requires a technical solution, the functional decision of the organization and esthetic. In this case the proportion "extreme and mean ratio" allows to solve variety of versatile tasks. Ancient geometra spoke: LOOK. And it is the main direction of a statement of material. Ключевые слова: золотое отношение, геометрия, круговые функции, пропорции в построении частей круга. Keywords: the gold relation, geometry, circular functions, proportions in creation of parts of a circle.
Красота Природы бесконечна в своем многообразии. Основой такого явления может быть только гармония частей общего мироздания в статичном и динамичном состоянии. В своей книге Курант Р. И Робинс Г. отметили: "… по мнению греческих математиков прямоугольник, стороны которого находятся в этом отношении, эстетически особенно приятен для глаза "[1.С.152].. Это отношение было названо «золотым» (и обозначается Ф (= 1,618) [2.С.21]. Указанная пропорция относится не только к прямоугольнику, но и к прямой ограниченной линии, разделенной в данном отношении и геометрическим фигурам, размеры частей которых находятся в данном отношении: правильные пятиугольники, спирали, объемные фигуры. Это примеры пропорции двух частей-отрезков. Зато в биологии имеется много примеров трехчастных пропорций. Такое совпадение характеристики объектов, где выполняется «золотое отношение», может быть обусловлено только фундаментальными свойствами пространства. В этих фундаментальных свойствах в обязательном порядке должны выполнятся функциональные зависимости.
Это является объективным математическим свойством. Основополагающими фигурами в математике являются круг, треугольник, четырехугольник, что в своем сочетании дают решения множества задач. Точки, принадлежащие вершинам геометрических фигур, которые определяются прямыми, при соответствующем построении принадлежат и окружностям (пересечение множеств). Это свойство позволяет производить поиск решения задачи, используя свойства круга R = const и свойства линий R = variabilis . Изменение угловой величины в круге будет определять величину хорды, а в построенном треугольнике, где основанием является искомая хорда, а боковыми сторонами является радиус окружности R = 1, отношение боковой стороны к основанию треугольника дает число Ф или золотое отношение.
В этом случае геометрические фигуры круг и треугольник имеют общие элементы, каждый из которых связан функционально с изменяющейся угловой величиной круга как аргументом. Изменение по определенной процедуре угловой величины, взятой как аргумент, определяет появление величин хорд, как функции, и их пропорций в " золотом отношении ". Выбор величины отсчета круговой функции равной 1/60 произведен по факторам совпадения величины дуги окружности и величины хорды, а величина сегмента круга равна 1/10 000 при радиусе круга R = 1. Приняв такую единицу отсчета угловой величины 1/60 величины круга как аргумента далее выполняется процедура вычисления функции, которой является соответствующая ей величина хорды: базовая величина (1/60), далее идет удвоение [2*(1/60)] — к этой величине далее будет суммироваться удвоение приращения — [2*(1/60)]+ 2*(1/60); [2*(1/60)]+ 2*(2*(1/60)) — (хорда составляет 0.618 при R=1); [2*(1/60)]+2*(2*2*(1/60)) — (хорда составляет 1.0 при R=1 ); [2*(1/60)]+2*(2*2*2*(1/60)) — ( хорда составляет 1.618 при R=1 или величина основания равнобедренного треугольника).
Графическое изображение функциональной зависимости пропорции «золотое отношение». Полученная последовательность величин хорд образуют части трехчастного деления, называемых вурфной пропорцией, которая вычисляется по формуле: W(a,b,c,) = (a+b)*(b+c)/b*(a+b+c) [2. С.54] и для рассмотренного варианта составляет (1,309). Особенностью архитектурного решения при трехчастном делении является то, что в
Древней Руси объект измерялся различными способами: длина измерялась одной единицей измерения (саженью), ширина — другой, высота — третьей, внутренняя часть — четвертой. (2.С81). Это решение позволяло создать гармонию восприятия внешней архитектуры и гармонию внутреннего нахождения в помещении не допуская резонансных явлений негативного характера. Кроме визуально-чувственного воздействия на биологические организмы вурфная пропорция присутствует на уровне элементарных частиц . Вурфные отношения наблюдаются в пропорциях спектральных линий водорода. Это серии Лаймана, Бальмера, Пашена.
Вурфные отношения наблюдаются в пропорциях величин радиусов, частот, энергий для орбит электрона в атоме водорода ( 2.С54 ). Выполнение вурфного отношения на уровне строения атомов вещества указывает на единообразие происходящих в Природе процессов и определяет направление дальнейшего исследования физики элементарных частиц. Многообразие в пропорциях хорд, полученных при вычислении по приведенному алгоритму подтверждает функциональные качества изменения круговой величины и получаемых величин хорд. Золотое отношение алгебраически записывается в виде: a/b = b/(a + b ) или b2 = a ( a + b ) или [A]2 = [B]*[C]. Эта структура алгебраической формулы имеет распространенный характер при изучении физических процессов. Необходимо отметить необычайные свойства в преобразовании относительно окружности которое называется инверсия. Инверсия преобразует точки, расположенные в окружности, на плоскость вне окружности и отрезки, ограниченные полученными точками, находятся в пропорции "золотое отношение". В инверсии базовая окружность радиуса r, центр инверсии O, точка на плоскости l и точка внутри базовой окружности k, находящиеся на одном луче, связаны зависимостью: Ok * Ol = r2 или Ok * ( Ok + kl )= r2. Алгебраическая форма записи золотого отношения и преобразования инверсии тождественны:
[C]* ([C + X]) = [C]*[B] = [A2] или = b2, или = r2. «Золотое отношение» при инверсии выполняется при расположении на луче точек геометрических фигур, характеризующих тождественные качества, например, особых точек треугольников, величина сторон которых выбрана в соответствии с указанной процедурой изменения круговой функции. Это подтверждает вывод о том, что геометрические построения, выполненные внутри окружности при изменении угловой величины, как аргумента по указанной процедуре, соотносятся с геометрическими построениями на плоскости и при этом выполняется пропорция «золотое отношение».
Таким образом гармония пропорций геометрических частей круга передается на плоскость и пространство и обосновывают вурфную пропорцию. Пропорция частей целого с названием «золотое отношение» в природе является одним из основ мироздания и одной из основных констант.
Список литературы
1. Курант Р., Робинс Г., Что такое математика?, М., «Просвещение», 1967, с.152.
2. Черняев А.Ф., «Золото» Древней Руси, М., «Белые Альвы», 1998, с.54. References 1. Kurant R. i Robbins G., What is mathematics ? Chto takoe matematika ? [Publ. Oxford University Press, London, New York, Toronto, 1941] Moscow, 1966, р.557(in Russian) 2. Chernjaev A.F., "Gold" of Ancient Russia, " Zoloto " Drevnej Rusi [ Publ. White Alvah, Moscow region, 1998], Moscow, 1998, p.142 (in Russion)
Молчанов Сергей Степанович Художник, Saatchi Art, Fine Art America П. Явoрницкого, д.99, кв.16, 49038 г.Днепропетровск, Украина egypy@yandex.ru
The functional properties of a proportion golden ratio Molchanov Sergey Artist, Saatchi Art, Fine Art America


 02.02.2017
02.02.2017 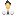 admin
admin
 Рубрика:
Рубрика:  Метки:
Метки: 


